×
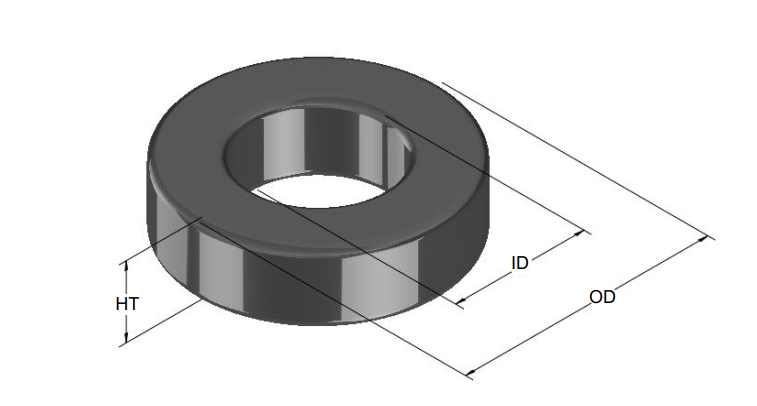
Wound Dimensions
This field displays an approximate estimate of the finished device dimensions,
not including header. It can be useful to verify whether the proposed design may
meet the application’s footprint or package size requirements.
The software uses these dimensions to
calculate a surface area for estimating temperature rise.
×
Impedance
This parameter is the nominal target impedance at the specified cutoff frequency, in Ω. The design algorithm converts those inputs to a target inductance according to $$ L_s = {Z_s \over (2πf)} $$ The assumption made is that Xs = Zs since the difference is negligible for low frequency.Voltage
This parameter is the RMS line voltage across both windings of the inductor (line Input as shown below).
Inductance
This parameter is the nominal target inductance, in mH.
For common mode chokes at a given line current, inductance is roughly proportional
to the Area Product (Magnetic Cross Sectional Area (Ae) x Winding Window Area (Wa).
Minimum inductance is specified on the core datasheet, generally at 20-30% less than the nominal value.
×
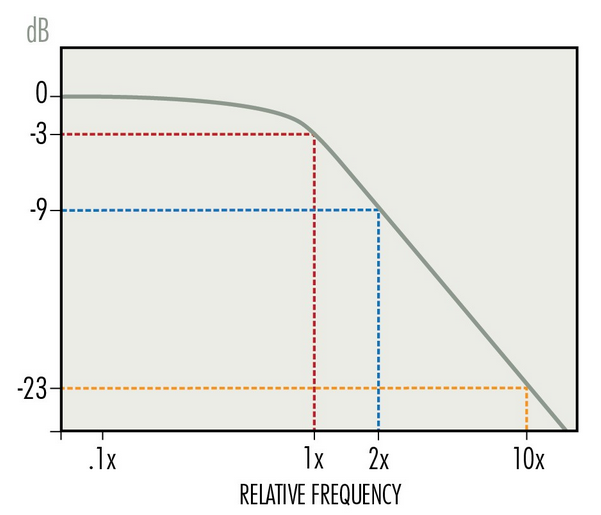For example, to achieve −23 dB attenuation at the switching frequency of a 100 kHz SMPS load, the target cutoff frequency would be 10 kHz. For CMN reduction of −23 dB at 50 kHz, the cutoff frequency is 5 kHz.
Cutoff Frequency
This parameter is the −3 dB (half-power) point of the low pass filter curve for the target common mode inductor, in Hz.
In conventional designs, the cutoff frequency is well below the most critical attenuation frequency. It means that two important design assumptions are true at the cutoff frequency: (1) the ferrite material is below its roll-off frequency and (2) the reactive impedance (Xs) is essentially the inductive impedance, and Xs dominates the total impedance (Zs).
For the software’s impedance input mode or voltage input mode, cutoff frequency is used to calculate the target inductance.
Common mode attenuation is achieved according to the curve below. The slope above the cutoff frequency is −20 dB per decade (10X increase in frequency.)
For example, to achieve −23 dB attenuation at the switching frequency of a 100 kHz SMPS load, the target cutoff frequency would be 10 kHz. For CMN reduction of −23 dB at 50 kHz, the cutoff frequency is 5 kHz.
×
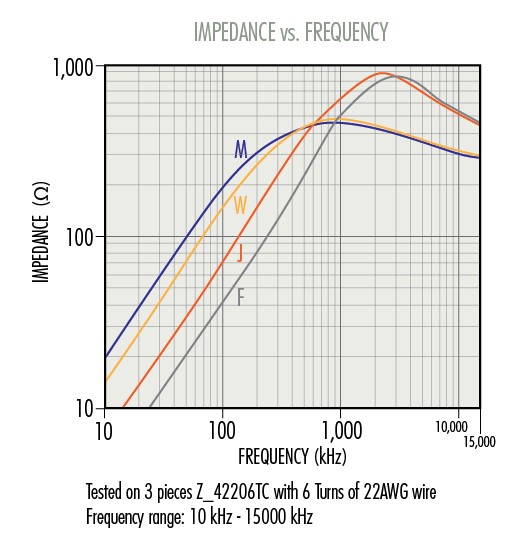
Materials Comparison
Magnetics' Common Mode Software features four ferrite materials suitable for use in CMN filters:
All are manganese zinc ferrites and in toroidal form offer optimized common mode attenuation
performance in the frequency ranges indicated.
The software also offers the option to make a first-cut design with nanocrystalline tape core
material. Due to the much higher permeability, it can be possible to achieve more impedance in
the same space compared with any ferrite. Tradeoffs are that the impedance curve may vary more
since permeability can vary more, and higher cost.
The primary design target for making the most effective common mode choke is to match the impedance
vs. frequency performance to the application requirement, which is the goal of this software. Secondary considerations include cost, size, winding sensitivity,
temperature stability, and maximum temperature. Therefore, a typical approach is to find several
solutions that meet the primary design target, and then analyze the secondary tradeoffs. See
References for more information on common mode choke design.
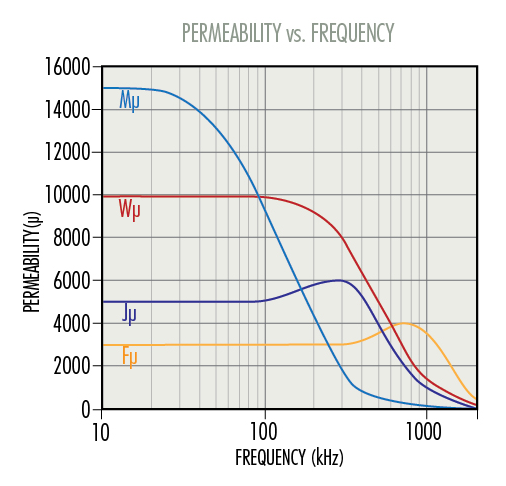Initial permeability and inductance are defined at frequencies below the material roll-off frequency,
which is lower for higher permeability materials, as shown in the first figure below. However, the
peak impedance frequency for each material is much higher than the permeability roll-off frequency.
This is because inductive impedance is proportional with frequency, and because reactive inductance
is not the only contributor to total impedance. As a result, for example, W material exhibits a
permeability roll-off frequency around 100 kHz, but W material is the superior choice for common mode
attenuation at frequencies up to more than 1 MHz, as reflected in the impedance curves in the
figure below.
Nanocrystalline performance as a function of frequency has different characteristics than ferrite,
and side-by-side comparison depends on the particular size, winding design, and impedance target.
| Material | F | J | W | M |
|---|---|---|---|---|
| Permeability (Nominal) | 3000 | 5000 | 10000 | 15000 |
| Typical Frequency use (for CMN filters) | 1 to 10 MHz | 500 kHz to 5 MHz | up to 3 MHz | up to 1.5 MHz |
Permeability, Impedance, and Frequency
Ferrite materials are offered in a wide range of initial permeabilities. Higher permeability means fewer turns to obtain a target inductance, resulting in a smaller device, lower DCR, lower winding capacitance, and potentially lower overall cost. A lower permeability ferrite may be selected for optimizing impedance at a higher frequency, wider temperature range, less winding stress sensitivity, or lower core cost. Initial permeability and inductance are defined at frequencies below the material roll-off frequency, which is lower for higher permeability materials, as shown in the figure below.
Initial permeability and inductance are defined at frequencies below the material roll-off frequency,
which is lower for higher permeability materials, as shown in the first figure below. However, the
peak impedance frequency for each material is much higher than the permeability roll-off frequency.
This is because inductive impedance is proportional with frequency, and because reactive inductance
is not the only contributor to total impedance. As a result, for example, W material exhibits a
permeability roll-off frequency around 100 kHz, but W material is the superior choice for common mode
attenuation at frequencies up to more than 1 MHz, as reflected in the impedance curves in the
figure below.
Nanocrystalline performance as a function of frequency has different characteristics than ferrite,
and side-by-side comparison depends on the particular size, winding design, and impedance target.
×
Schematic of an EMI Filter
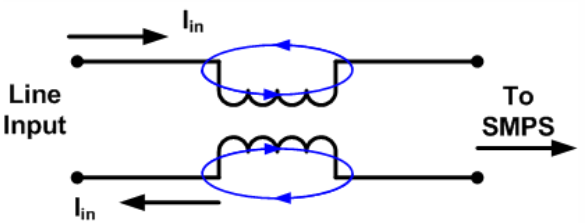Filter Reaction to Input Line Current
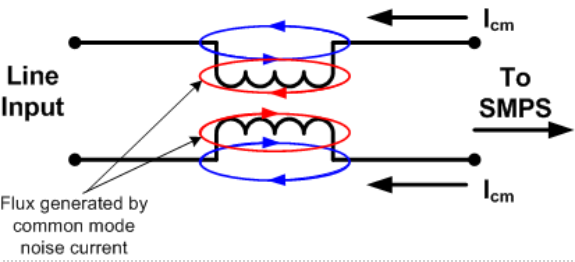Filter Reaction to Common Mode Noise Current
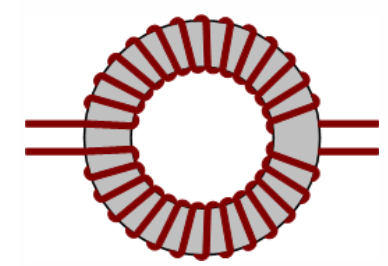Common Mode Inductor Winding Arrangement
General Information
EMI Filters
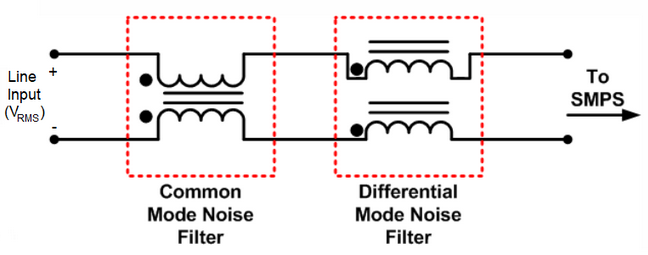
Switched mode power supplies (SMPS's) typically generate high frequency noise that must be attenuated. These unwanted electrical signals can pass from the power supply onto the input power lines. Other electronic equipment sharing the lines may be subjected to this conducted noise, which can cause errors and possibly even catastrophic faults in connected equipment. An EMI noise filter inserted at the SMPS power input (see figure below) can block this type of interference. This diagram shows a differential noise filter and a common mode noise filter in series. In many cases the common mode filter is used alone, as it can often eliminate as much as 90% of the unwanted noise (including some differential mode noise, because even a nearly ideal common mode choke will exhibit a small differential impedance).
Schematic of an EMI Filter
Common Mode Filters
In a common mode noise (CMN) filter each winding of the inductor is connected in series with one of the input power lines. The connections and phasing of the inductor windings are such that the flux created by each winding appears to cancel (actually sums to zero within the core material) the flux generated by its opposing winding. The insertion impedance of the inductor to the input power line is therefore negligible. The two figures below illustrate both the flux generated by the power lines and that induced by any common mode noise present on the lines. While 'power line' flux sums to zero (often thought of as 'canceling') because of its opposing nature, the common mode flux is left unopposed and therefore encounters the high reactive impedance of the core material. This high impedance offers filtering action against the common mode noise.
Filter Reaction to Input Line Current
Filter Reaction to Common Mode Noise Current
Current Filter Reaction to Common mode noise toroidal cores are most popular for CMN
filters as they are inexpensive and have very low leakage flux with high CMN
impedance. Toroids may have higher winding costs than bobbin wound shapes such as
EE and pot cores. However, the higher inductance allowed by having no inherent air
gap at a mating surface can add as much as 30% more impedance for the same core
material. It is typical for a non-metallic divider to be inserted between the two
windings for mains isolation, and the wound unit is epoxied or the leads mounted to a
printed circuit header for attaching to a PC board.
An illustration is below. The device is typically called a common mode choke or
common mode inductor.
Common Mode Inductor Winding Arrangement
Design Method Summary
The basic parameters needed to select a core for use as an effective common mode
inductor are input line current (I, in ARMS),frequency (f, in Hz),
and series impedance
(Zs, in Ohms). Although many designers specify CMN designs based on inductance
instead of frequency and impedance, these specifications can be regarded as
equivalent to one another (see equations below and Help notes regarding the
software's design modes). The current input, along with an expected current
density, determines the wire size. Conservative current density values
(e.g. 400 A/cm²) imply larger wire sizes that will not significantly heat up.
More aggressive values (800 A/cm² or higher) allow a smaller inductor design,
but with the potential for more heat build-up. The impedance of the inductor is
normally specified as a minimum at a given frequency. This frequency is usually
low enough to allow the (very important) assumption that the inductive reactance,
Xs, supplies essentially all of the impedance. Consequently, the inductance may
be calculated from:
Ls=Xs2πf
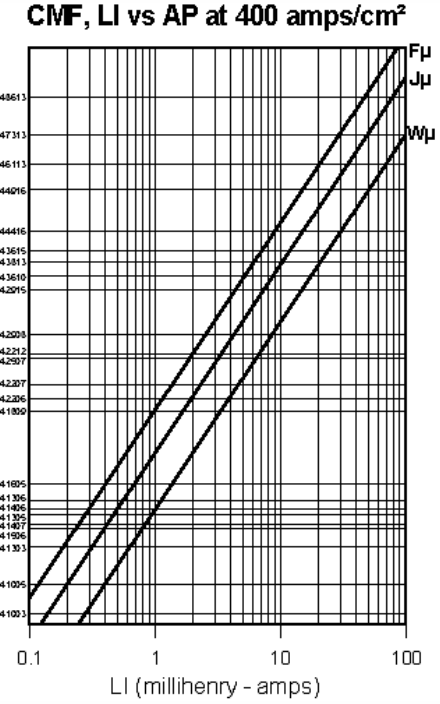
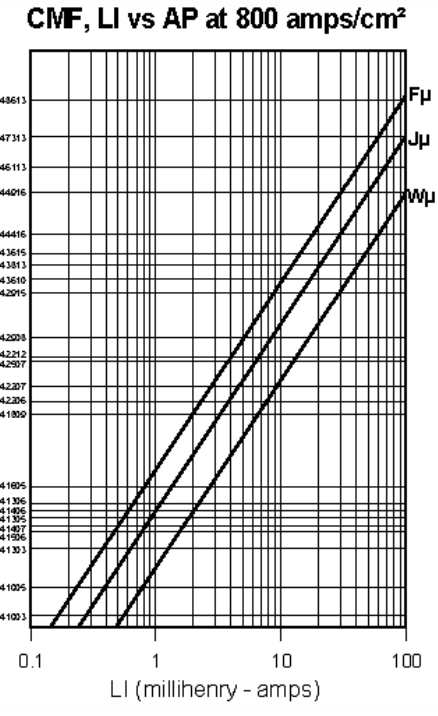
the inductance and current known, analytical (such as this design software)
or graphical (as shown below) design tools may be used to select the core size based
on the LI (really LsI ) product, with L in mH and I in Amps.
Both the curves above and the design software use an algorithm that finds a core
size large enough to accommodate the necessary number of turns while maintaining
a 30° arc of free space between the start and stop of both windings.
This will allow enough room for an isolating spacer to be deployed between the
windings. The wire size (AWG) is then calculated using the following equation based
on the current density (Cd) selected.
$$ AWG = -4.31 \ln ( {1.889 I \over C_d } ) $$
To complete the design, the number of turns per winding is determined from
the core's AL value as follows:
$$ N = {L_s 10^6 \over A_L}^{1 \over 2} $$